Many of you already know that to in computer systems, to represent the negative numbers we use what is known as 2’s complement. In this article I will try to explain where it came from.
Introduction
A binary representation of a number of a sequence of bits (ones and zeroes) where each position represent the value 2 to the power of that position; the rightmost digit represent 20, the next digit represent 21 and so on. The next figure shows a sample 8-bit representation with the value associated with each position.
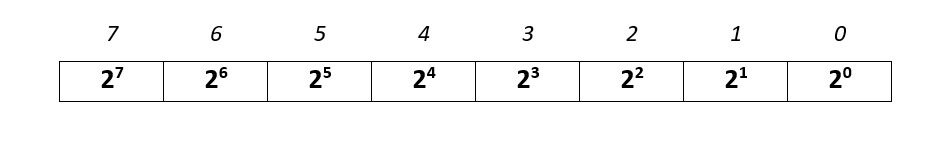
So, if we have a binary number 0101, the right most digit is multiplies by 20, the next digit will be multiplied by 21, the digit thereafter is multiplied by 22 and so on.
0101 = 1 x 20 + 0 x 21 + 1 x 22 + 0 x 23 = 1 + 0 + 4 + 0 = 5
For N-bits the range of numbers that can be represented are 0 to 2N. In the above example, we have 8 bits and so we can represent numbers from 0 (00000000) to 28-1=255(11111111)
What about Negative Numbers?
This works great for positive numbers but how can we use the same notation to represent negative numbers and be able to distinguish them from negative numbers.
One simple yet efficient solution to dedicate the leftmost bit to indicate the sign of the number (0 indicates a positive number with 1 indicates a negative number).
For example, we know the binary representation of five is 101, so to store 5 and -5 in the 8 bit the representation would be as follows:

Notice that now we represent a different range of number from -127 (111111111) to 127 (01111111)
This is good but it causes some inefficiencies when performing arithmetic operations (we will focus on addition and subtraction) because we need to look at the leftmost bit (most significant bit) to determine the sign of the number and then perform the desired operation.
Can we come up with a better representation?
A first step is to use addition to represent subtraction as well. What I mean is if we have A – B then this can be written as A + (-B). Hence, we can convert subtract operations to addition operation of the one number and the negative of the other (A – B is addition of A and –B). This way we can simply the logic of our operations but this relies on a better representation for negative numbers that would achieve the correct result. Consider the following example:
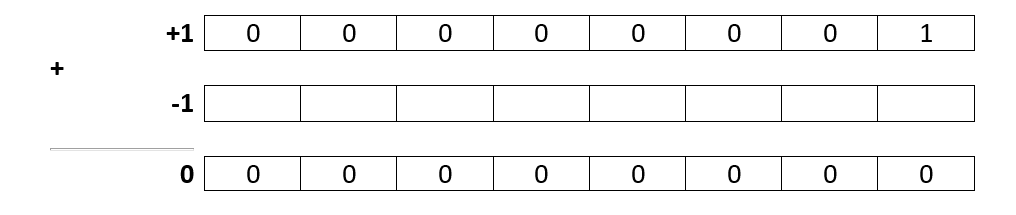
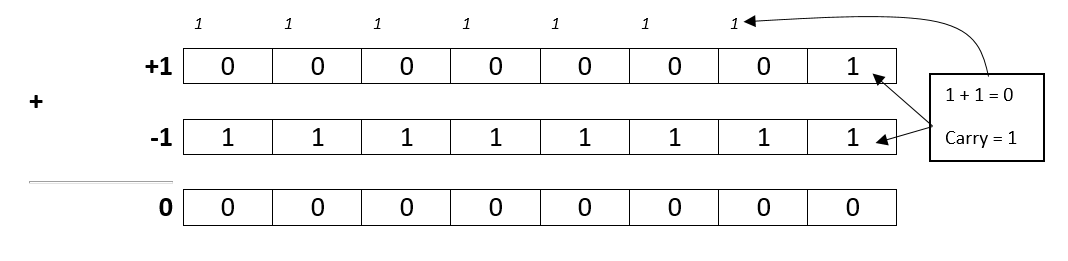
We know that (+1) is represented as (00000001) and Zero is represented as (00000000), so what would be a good representation of (-1) such that (+1) + (-1) = (0).
We Know that in binary addition, 0 + 0 = 0, 0 + 1 = 1, 1 + 1 = 0 (carry 1). If we set the rightmost bit to 1 then the addition is zero with carry 1. If we set the next bit to 1 then the addition is 1 + 0 + carry 1 = 0 (carry 1) and so on. So if we set all bits to 1 we will achieve the desired effect.
Consider a general number A, we want to find –A such that A + (-A) = 0. This can be rewritten as: -A = 0 – A, which can further be written as –A = (1 + (-1)) – A, as we established that 0 = 1 + (-1). As such, -A = 1 + (-1 – A)
To illustrate, what is the result of 1 – A? for individual bits we know that 1 – 0 = 1 and 1 – 1 = 0 i.e it is the inverse of the bit so 1 – A (~A) is the bitwise inverse of A i.e. each bit is flipped. The bitwise inverse of A (~A) is known as 1’s complement.rr
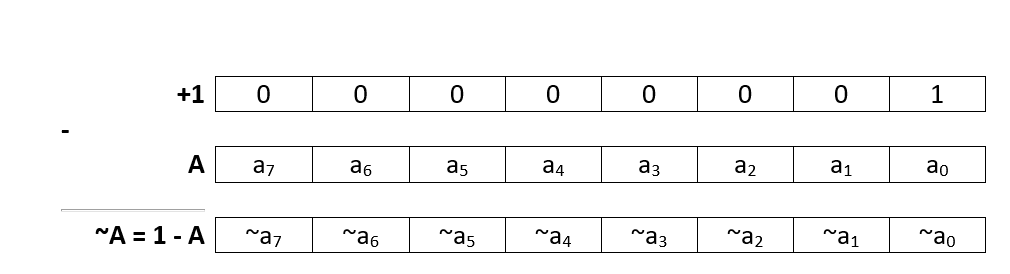
Back to our formula -A = 1 + (-1 – A) = -A = 1 + ~A. As such, the negative of a number can be found by finding the bitwise inverse and then adding one to the result and this is known as 2’s complement.
For example, -5 is represented using the 2’s complement of 5
5 = 00000101 1’s complement (flip each bit) : 11111010 2’s complement (add 1 to 1’s complement):
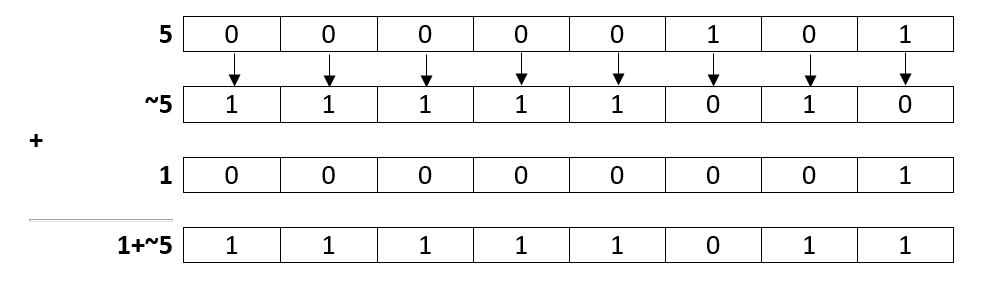
Let’s give it a try:
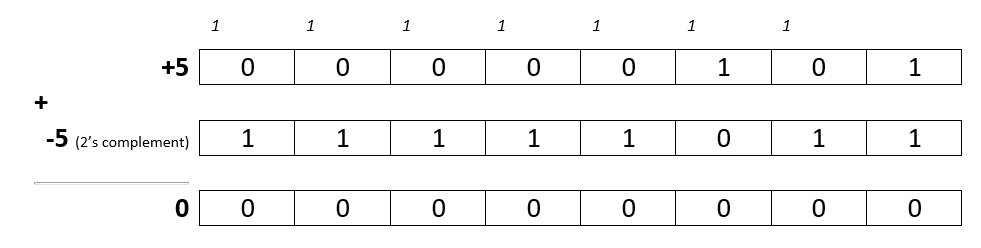
Conclusion
In 2’s complement representation, positive numbers are represented as themselves while negative numbers are represented by the 2’s complement of their positive value. The 2’s complement has the advantage that the addition and subtraction are identical to those for unsigned numbers as long as the inputs are represented in the same number of bits.