Suppose we we have sorted array and we are interested in finding a particular element. There are a number of ways we can go about it.
Let’s give a concrete example, The array is of length $\mathcal{L}$ containing the following elements:
[
283, 293, 307, 311, 313, 317, 331, 337, 347, 349, 353, 359, 367, 373, 379, 383, 389, 397, 401, 409,
419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499, 503, 509, 521, 523, 541,
547, 557, 563, 569, 571, 577, 587, 593, 599, 601, 607, 613, 617, 619, 631, 641, 643, 647, 653, 659,
661, 673, 677, 683, 691, 701, 709, 719, 727, 733, 739, 743, 751, 757, 761, 769, 773, 787, 797, 809,
811, 821, 823, 827, 829, 839, 853, 857, 859, 863, 877, 881, 883, 887, 907, 911, 919, 929, 937, 941
]
and we are interested in finding 467 (which resides at index 31). In our diagrams we will follow the same notation used in Information Retrieval Implementing and Evaluating Search Engines excellent book.
Linear Search
The simplest solution is to scan the array in a linear fashion until we find it.
def linear_search[A](arr: List[A], x: A) -> int:
i = 0
while i < len(arr) and arr[i] <= x:
if arr[i] == x:
return i
i = i + 1
# if we reach here then the element is not present
return -1
Since the array is already sorted if we reach an element bigger than our target we can conclude that the target is not found in the array and we can terminate.
The diagram below shows how the linear search would go, at each step we hop one step until we find our target.
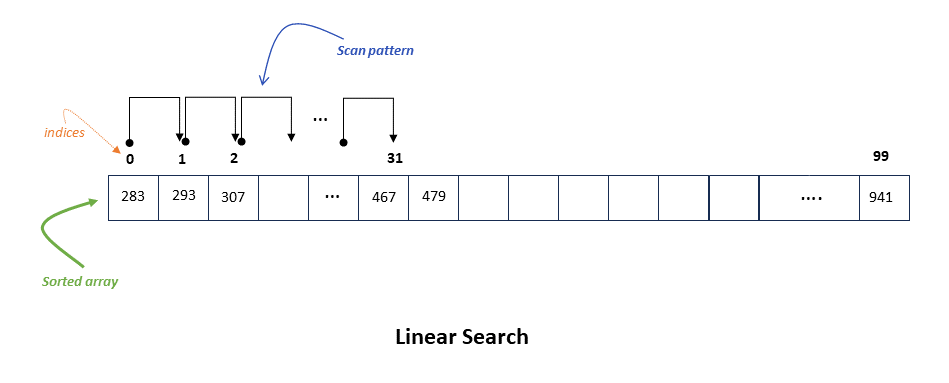
In the worst case we would need to scan the entire array which makes our time complexity $O(\mathcal{L})$
Binary Search
A faster approach is binary search where we try to successively half the interval to scan until we find the target element. At each step we compare the target value with the middle element. If they are not equal and because the array is sorted we can eliminate half the array and search in the remaining half.
def binary_search[A](arr: List[A], x: A, start:int|None=None, end:int|None=None) -> int:
if start is None:
start = 0
if end is None:
end = len(arr)
if end >= start:
mid = start + (end - start) // 2
# If the element is present at the middle
if arr[mid] == x:
return mid
# If the element is smaller than mid, then it can only be present in the left sub-array
if arr[mid] > x:
end = mid - 1
# Else it can only be present in the right sub-array
else:
start = mid + 1
return binary_search(arr, x, start, end)
# if we reach here then the element is not present
return -1
The diagram below shows how the binary search would go, at each step we hop by half the length of the sub-array until we find our target.
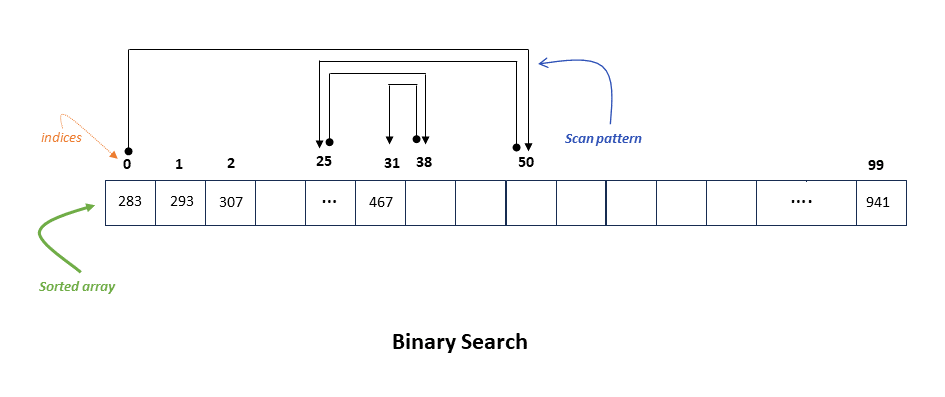
Because we are halving the array at each step, binary search runs in logarithmic time with complexity $O(\log(\mathcal{L}))$
Galloping Search: Combining Them Together
Galloping Search (a.k.a. exponential search) is an idea that tries to combine both approaches:
- First, we do a linear scan in exponentially increasing steps (gallops) until we hit an element larger than our target value.
- Then, we do a binary search in the range between the last two jumps which is a smaller range than doing a binary search on the entire array.
def galloping_search(arr: List[A], x: A) -> int:
n = len(arr)
# if x is present at first location
if arr[0] == x:
return 0
# Find range for binary search by repeated doubling
i = 1
while i < n and arr[i] <= x:
i = i * 2
return binary_search( arr, i // 2, min(i, n-1), x)
The diagram below shows how the galloping search would go. First, we hop in exponentially increasing steps {1,2,4,8,16,…} until we pass our target element. Then we do binary search between the previous and current position.
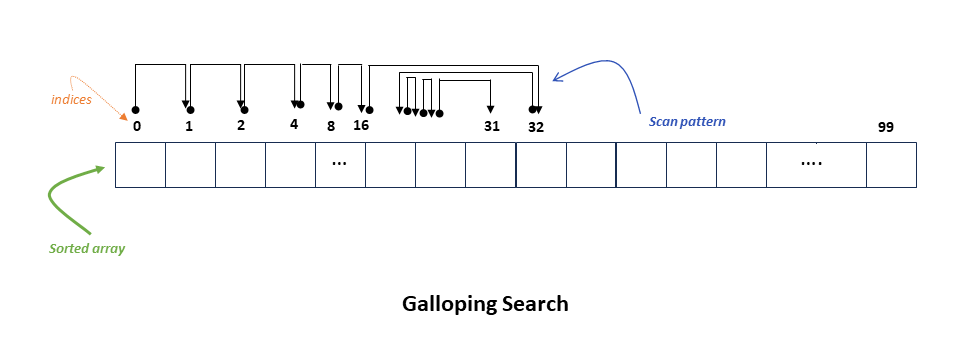
Galloping search also runs in logarithmic time but with complexity $O(\log(\mathcal{l}))$ where $\mathcal{l}$ is the index of the target element.
Galloping search can be faster if the target element is near the beginning of the array. This can be useful if we want to perform repeated searches i.e., find all elements in one array in another array.