PageRank is an algorithm used to rank web pages in search engines results. It was named after, one of the founders of Google, Larry Page.
Introduction
PageRank is an algorithm used to rank web pages that relies on two ideas:
- counting the number of in-links a page has where the more in-links the higher the rank.
- In-links from pages having a high rank should be worth more than in-links from pages having a low rank.
This definition seems recursive because if a page A is linked to by three other pages B,C,D then in order to determine the PageRank of page A we need to also know the PageRank of B,C,D. As such, each page distributes its PageRank score equally on its out-links, the more out-links a page has, the less the share of each link. In our earlier example, the PageRank $PR(A) = \frac{PR(B)}{L(B)}+\frac{PR(C)}{L(C)}+\frac{PR(D)}{L(D)}$ where $L(x)$ is the number of out links from page $x$.
More generally, we can express page rank as :
$$PR(p) = \sum \limits_{q \in In(p)} \frac{PR(q)}{L(q)}$$
where $In(p)$ is the set of in-links to page $p$.
We can think of the problem as a surfer who follows the links randomly from a given page. However, the problem with this definition is that some pages do not have any out-links (a sink page) which can make our algorithm get stuck and that is why we need a better model.
The Random Surfer Model
Similar to how most people surf the web, on a given web page you choose to follow one of the links on the links on the page. If you reach a page without any links (a sink page) then you simply randomly restart on a new page on the web Furthermore, every once in a while, you get bored of following the link and you decide to jump to a totally new page.
In mathematical notation, let $c$ be the probability that the surfer will continue following the links while $(1-c)$ is the probability that the surfer will get bored and jump to a random page. A good value for $c = 0.85.$ This time PageRank score is a combination of the contribution of PageRank scores of the in-links and the contribution of randomly landing on this page when the surfer is bored.
$$ \begin{equation} \label{page rank} PR(p) = c \times \sum \limits_{q \in In(p)} \frac{PR(q)}{L(q)} + (1-c) \times \frac{1}{N} \end{equation} $$
We can think of the PageRank score $PR(p)$ of a page $p$ as the probability that a random surfer will be at page $p$ at a given point in time. In this interpretation, the PageRank score will be between 0 and 1 and since the surfer has to be on some page at any given time and the sum of the PageRank scores of all the pages sums to 1.
The Algorithm is as follows:
- Assign each node an initial page rank
- repeat until convergence: calculate the page rank of each node using equation $\eqref{page rank}$
Worked Example
Consider this example, where we have four web pages pointing to each other as shown in the figure below. Intuitively, Page C has 3 in-links so it should have the highest PageRank and page D should be last because it does not have any in-links.
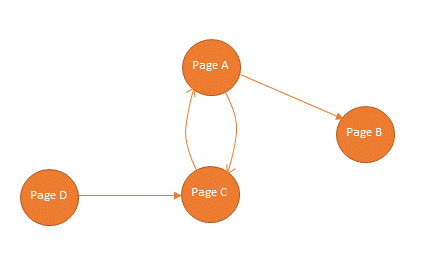
We can write the PageRank score of each page as follows:
$$ \begin{aligned} PR(A) &= c \times \frac{PR(C)}{1} +\frac{(1-c)}{4} \newline PR(B) &= c \times \frac{PR(A)}{3} + \frac{(1-c)}{4} \newline PR(C) &= c \times \left(\frac{PR(A)}{3} + \frac{PR(B)}{1} + \frac{PR(D)}{1} \right) + \frac{(1-c)}{4} \newline PR(D) &= c \times \frac{PR(A)}{3} + \frac{(1-c)}{4} \newline \end{aligned} $$
Matrix Representation
To make solving the above equations easier we can write them in matrix format. We will not go into all the mathematical details but we can write the equation as the sum of two matrices, the first matrix is very similar to the adjacency matrix of the original graph while the second matrix is just a constant matrix.
$$\begin{bmatrix} PR(A) & PR(B) & PR(C) & PR(D) \end{bmatrix} = \left(c \times \begin{bmatrix} 0 & 0.5 & 0 & 0 \newline 0 & 0 & 1 & 0 \newline 1 & 0 & 0 & 0 \newline 0 & 1 & 0 & 0 \end{bmatrix} + \frac{(1-c)}{4} \times \begin{bmatrix} 1 & 1 & 1 & 1 \newline 1 & 1 & 1 & 1 \newline 1 & 1 & 1 & 1 \newline 1 & 1 & 1 & 1 \end{bmatrix} \right) $$
We can then use Power Iteration method to solve this problem Let $c = 0.85$ and suppose we initialize
$$ \begin{bmatrix} PR(A) & PR(B) & PR(C) & PR(D) \end{bmatrix} = \begin{bmatrix} 1.0 & 0 & 0 & 0 \end{bmatrix} $$
| Page | Iteration 1 | Iteration 2 | Iteration 3 | Iteration 4 | … | Iteration 12 |
|---|---|---|---|---|---|---|
| Page A | 1.0 | 0.0375 | 0.4306250 | 0.41707812 | 0.36124157 | |
| Page B | 0.0 | 0.4625 | 0.0853125 | 0.25239062 | 0.22300072 | |
| Page C | 0.0 | 0.4625 | 0.4465625 | 0.29303125 | 0.37825770 | |
| Page D | 0.0 | 0.0375 | 0.0375000 | 0.03750000 | 0.03750000 |
Python Implementation
We can easily implement the iterations of power method in a couple of lines of python.
import numpy as np
def page_rank(adj_matrix):
# parameters
num_pages = adj_matrix.shape[0]
c = 0.85
uniform_prob = 1.0/num_pages
epsilon = 1e-5
# transition probability
transition_matrix = c * adj_matrix + (1-c) * np.full((num_pages, num_pages), uniform_prob)
# initialize page rank
pr = np.full((1, num_pages), uniform_prob)
pr_new = np.matmul(pr, transition_matrix)
while np.sum((pr_new - pr)**2) > epsilon:
pr = pr_new
pr_new = np.matmul(pr, transition_matrix)
return pr
Conclusion
In this post, we described the PageRank algorithm. We then described the random surfer model and the interpreting PageRank as a probability. Later we described the algorithm steps and discussed how to use power iteration to solve the recursive equations.