Attackers maintains fake accounts to use them for various reasons, for example, in a social media website, attackers could use them to post content to push a certain ideas. Another example in online retail where attackers use fake accounts to add fake reviews to improve the visibility of certain product.
In this post we will cover random walk based model proposed in Random Walk based Fake Account Detection in Online Social Networks to detect fake accounts.
The paper proposes a random-walk based method to detect fake accounts. The first step is to build a graph $G= (V,E)$ where a node $v$ represents a user and an edge $(u,v)$ indicates an interaction or a relationship between $u$ and $v$. For instance, the the online reviews setup an edge could mean $u$ and $v$ both reviewed the same product. The weights on the edge could depend on the strength of the relation/interaction (generally application dependent).
Detecting fake accounts or abusers is equivalent to assigning each user one of the labels benign or sybil. Where a benign label is for normal users and a sybil label is for abusers. In any system some users are verified (they can be trusted) while other others are known abusers (e.g., blocked by moderators). Hence, some users are already labeled and in order to label the remaining users we need to:
- Add two additional nodes to the graph; one for the benign label and the other for the sybil label.
- Add an edge between each labeled user and the corresponding label
The process is depicted in the example below:
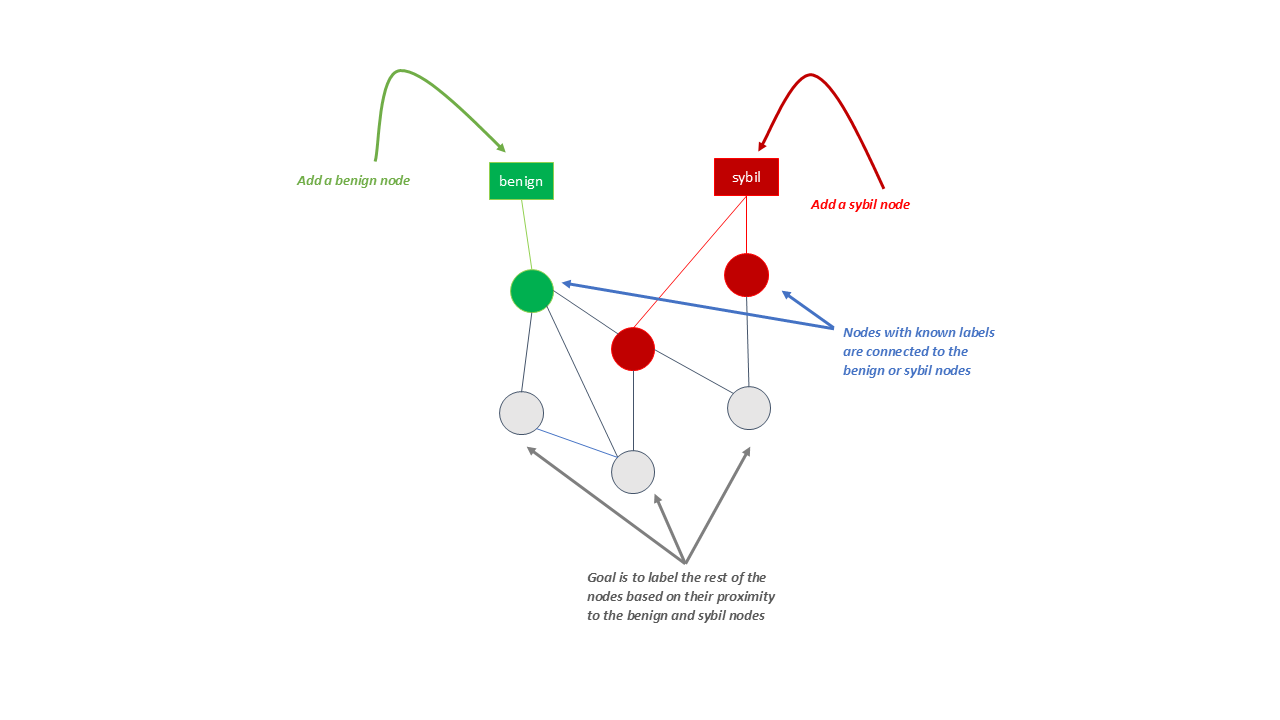
Then, we want to generate a badness score that represents how likely a node is a sybil. Intuitively, the closer a node is to the sybil label, the higher its badness score should be.
Each node $u$ has a set of neighbors denoted as $T_u$, each node is connected by an edge with weight $w_{uv}$. We define the weighed degree of node $u$ as $d_u = \sum_{v\in T_u}w_{uv}$. The badness score of a node $u$ is defined as:
$$ p_u = \sum_{v \in T_u} \frac{w_{uv}}{d_u} p_v $$
i.e., the badness score of a node $u$ is a weighted sum of the badness score of its neighbors. Because the badness score of the nodes in $T_u$ also depends on their neighbors we need an iterative algorithm such that at the $t$th iteration the badness score is:
$$ p_u(t) = \sum_{v \in T_u} \frac{w_{uv}}{d_u} p_v(t-1) $$
The algorithm keeps iterating until the change in the badness score between two iterations does not change. The algorithm is summarize below:
Input: Graph G = (V,E)
Output: badness score for every user node u.
Initialize:
$\hspace{2em}$ $p_u(0) = 0.5$ for every user node u.
$\hspace{2em}$ $p_{\text{benign}}(0) = 0$
$\hspace{2em}$ $p_{\text{sybil}(0)} = 1$
$\hspace{2em}$ $i = 1$
while $p_u(t) - p_u(t-1) > \epsilon$ and $ i < \text{Iters}$:
$\hspace{2em}$for each user u do:
$\hspace{4em} p_u(t) = \sum_{v\in T_{u}}\frac{w_{uv}}{d_{u}}p_v(t-1)$
$\hspace{2em}$ $i = i + 1$
This is very similar PageRank Random Surfer Model and be implemented in a few lines of code:
def power_iter(adjacency_matrix, max_iter, tol=1e-6):
M = adjacency_matrix
n = adjacency_matrix.shape[0]
# we initialize all nodes with badness score of 0.5
x = 0.5 * np.ones((n))
x[BENIGN] = 0 # benign node has a score of 0
x[SYBIL] = 1 # sybil node has a score of 1
i = 0
while i <= max_iter:
x_last = x
x = M*x
x = x
# check convergence, l1 norm
err = np.absolute(x - x_last).sum()
if err < n*tol:
break
i+=1
return x
The random walk based model presents a compelling and simple approach to detecting fake accounts in online settings by building the interaction graph we were able to trace the patterns and interactions associated with fraudulent behavior. Moreover, it can leverage both positive (sybil) and negative (benign) samples in the detection process making it more robust.